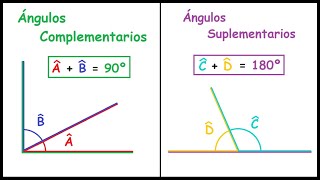
La principal diferencia entre los ángulos complementarios y suplementarios radica en sus sumas: los ángulos complementarios suman 90 grados, mientras que los ángulos suplementarios suman 180 grados. Esta distinción es fundamental en la geometría y tiene aplicaciones prácticas en diversas disciplinas.
En el estudio de la geometría, es fundamental comprender la diferencia entre los ángulos complementarios y suplementarios. Estas dos categorías de ángulos son conceptos básicos pero esenciales para el entendimiento de diversas aplicaciones matemáticas. A continuación, se detallará de manera exhaustiva y profesional las características y diferencias entre los ángulos complementarios y suplementarios.
Tabla de contenidos
Toggle¿Qué son los ángulos complementarios?

Los ángulos complementarios son aquellos cuyos valores suman exactamente 90 grados. En términos matemáticos, si se tienen dos ángulos A y B, y se cumple que A + B = 90°, entonces estos ángulos son complementarios. Esta propiedad es una característica clave en la resolución de problemas geométricos y trigonométricos.
Propiedades de los ángulos complementarios
Algunas propiedades importantes de los ángulos complementarios incluyen:
- Los ángulos complementarios pueden ser adyacentes o no adyacentes.
- Si dos ángulos son complementarios y uno de ellos es un ángulo recto (90 grados), el otro ángulo deberá ser de 0 grados, lo cual es una condición especial.
- La relación de complementariedad se mantiene independientemente de la orientación de los ángulos.
¿Qué son los ángulos suplementarios?
Por otro lado, los ángulos suplementarios son aquellos cuyos valores suman exactamente 180 grados. Matemáticamente, si se tienen dos ángulos C y D, y se cumple que C + D = 180°, entonces estos ángulos son suplementarios. Este concepto es esencial en el estudio de polígonos y otras figuras geométricas.
Propiedades de los ángulos suplementarios
Algunas propiedades destacadas de los ángulos suplementarios incluyen:
- Los ángulos suplementarios pueden ser adyacentes, formando una línea recta, o no adyacentes.
- Si un ángulo es agudo (menos de 90 grados), su ángulo suplementario será obtuso (más de 90 grados), y viceversa.
- En un triángulo, los ángulos internos que suman 180 grados son un ejemplo de ángulos suplementarios.
Diferencias clave entre ángulos complementarios y suplementarios
Para entender de manera clara la diferencia entre los ángulos complementarios y suplementarios, es crucial comparar sus características y propiedades.
Suma de los ángulos
La diferencia principal radica en la suma de sus medidas:
- Los ángulos complementarios suman 90 grados.
- Los ángulos suplementarios suman 180 grados.
Tipos de ángulos involucrados
Los ángulos complementarios generalmente involucran ángulos agudos, ya que la suma no puede superar los 90 grados. En cambio, los ángulos suplementarios pueden involucrar ángulos agudos y obtusos, ya que su suma debe ser de 180 grados.
Aplicaciones geométricas
En aplicaciones prácticas:
- Los ángulos complementarios son cruciales en problemas relacionados con triángulos rectángulos y trigonometría básica.
- Los ángulos suplementarios son esenciales en el estudio de polígonos, especialmente en la determinación de ángulos internos y externos.
Comparación entre ángulos complementarios y suplementarios
Para resumir, se presenta una lista detallada con las principales diferencias entre ambos tipos de ángulos:
- Suma de ángulos:
- Complementarios: 90 grados.
- Suplementarios: 180 grados.
- Tipos de ángulos:
- Complementarios: Generalmente agudos.
- Suplementarios: Pueden ser agudos y obtusos.
- Aplicaciones:
- Complementarios: Triángulos rectángulos y trigonometría.
- Suplementarios: Polígonos y ángulos internos/externos.
- Propiedades geométricas:
- Complementarios: Pueden ser adyacentes o no.
- Suplementarios: Pueden formar una línea recta o no.
Cada tipo de ángulo tiene sus propias características y aplicaciones, lo que los hace únicos y fundamentales en el estudio de la geometría.